Modelli di ottimizzazione del Revenue: la programmazione lineare
Programmazione lineare: metodo grafico, esercizi e definizione del modello di ottimizzazione del Revenue
Ci sono molti modelli di ottimizzazione del Revenue. Alcuni complicati altri meno e altri ancora gelosamente custoditi da alcune grandi aziende.
Noi ci occuperemo di alcuni modelli:
- Programmazione lineare
- Modello “ABC”
- Modello “Bid Price”
- Modello “EMSR”
- Il modello di Karaesmen e van Ryzin
- L’approccio del ricavo atteso
È utile conoscere alcuni accenni di questi modelli perché danno l’idea della difficoltà e delle semplificazioni che si devono inevitabilmente fare nella costruzione di programmi e modelli per questo genere di attività.
Il primo modello che andremo ad analizzare è il modello che si basa sulla “programmazione lineare”.
Programmazione lineare definizione
Ma prima di spiegare il modellino devo introdurre i concetti base della programmazione lineare:
infatti tutti si staranno chiedendo, cos’è la programmazione lineare? Facciamo un salto su Wiki e scopriamo la definizione di Linear Programming:
“Linear programming is a technique for the optimization of a linear objective function, subject to linear equality and linear inequality constraints. Given a polyhedron (for example, a polygon), and a real-valued affine function defined on this polyhedron, a linear programming method will find a point on the polyhedron where this function has the smallest (or largest) value if such point exists, by searching through the polyhedron vertices.”
Ma non spaventatevi questa è la definizione formale, in parole semplici la programmazione lineare è una tecnica per risolvere problemi di ottimizzazione lineari. Si cerca di ottimizzare, quindi massimizzare o minimizzare a seconda dei casi, una funzione lineare quando ci sono dei vincoli. Un tipico esempio di programmazione lineare è composto da una funzione obiettivo e da una serie di vincoli. Una tipica funzione obiettivo è la seguente:
Dove c_i è il vettore dei coefficienti e x_i è il vettore delle variabili. La forma canonica è scritta nel seguente modo:
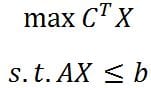
Dove X è il vettore delle variabili da determinare, C e b sono i vettori dei coefficienti noti e A è la matrice dei coefficienti noti. L’equazione sotto (s.t.=subject to) rappresenta i vincoli che la funzione obiettivo deve rispettare.
Programmazione lineare: metodo grafico e risoluzione geometrica
Questi problemi si possono risolvere per via geometrica o per via matematica attraverso appositi algoritmi (il più utilizzato è l’algoritmo del simplesso ma ce ne sono molti altri) oopure attraverso programmi come il risolutore di Excel. In questo link trovato in questo blog trovate un esempio di come utilizzare Excel per la risoluzione di problemi di programmazione lineare. Il metodo più semplice e intuitivo (ma che si può utilizzare solo quanto i vincoli sono pochi) per risolvere un problema di programmazione lineare è utilizzare la risoluzione per via geometrica.
Preferisco spiegare questa tecnica perché una volta capita questa riuscirete ad avere l’intuizione per capire anche l’algoritmo del simplesso (ma in caso farò un post dedicato a quello).
Allora andiamo con calma, vediamo la risoluzione per via geometrica:
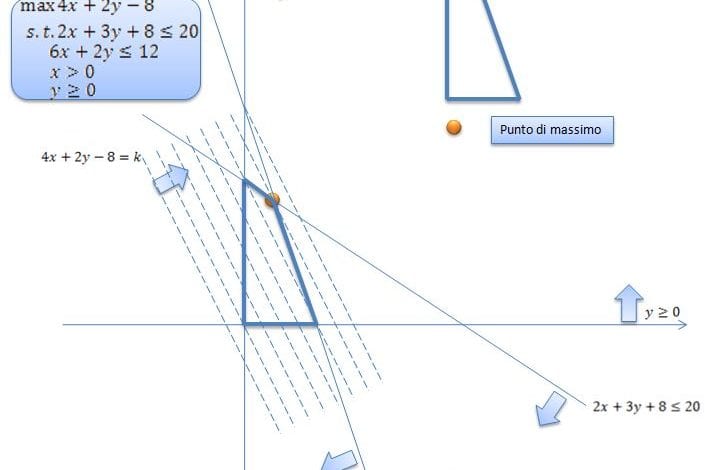
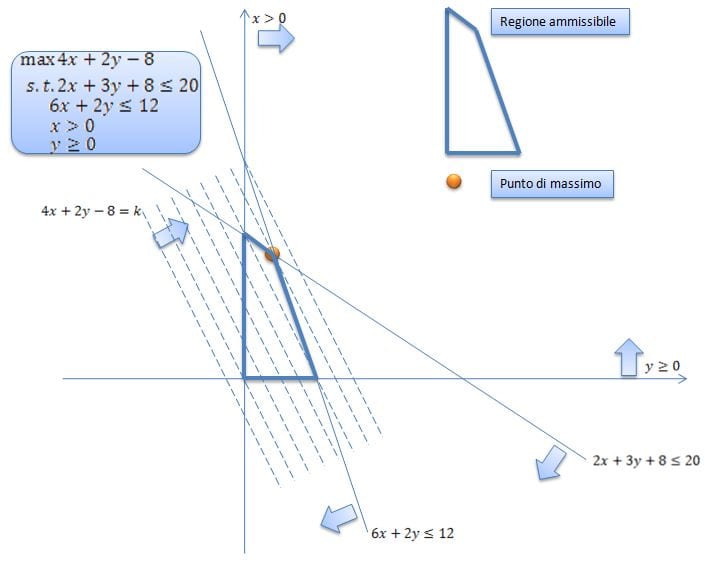
Per risolvere in via geometrica un problema di programmazione lineare dobbiamo costrure un grafico. In questo grafico dobbiamo disegnare la “feasible region” (la regione ammissibile) che è ricavata disegnando tutti i vincoli del nostro problema. Successivamente bisogna disegnare le curve di livello (possono essere un fascio proprio o impropio). L’andamento delle curve di livello ci fa capire quale punto all’interno della regione ammissibile massimizza la funzione obiettivo. Proviamo a fare un grafico/esempio per esplicitare la situazione:
Dal grafico che ho disegnato vediamo come si disegna la “regione ammissibile” e vediamo inoltre che per trovare il punto di ottimo dobbiamo disegnare il fascio di rette (4x +2y-8=k “fascio improprio”) che definiscono l’insieme delle curve di isoprofitto (oppure curve di livello). Fatto questo vediamo l’andamento di queste rette tratteggiate e scopriamo qual’è il punto in cui si massimizza la funzione obiettivo.
NB. Le soluzioni di un qualsiasi problema di programmazione lineare si trovano sempre all’interno della regione ammissibile e in quella parte di piano individuata dai vincoli (è detto insieme poliedrale). Questo insieme è convesso. La soluzione del nostro problema è un punto (ma può essere anche un insieme di punti) che massimizzi o minimizzi la funzione obiettivo. Se il problema ha soluzione questa la si trova in uno dei vertici della regione ammissibile, se invece il problema ha più soluzioni almeno uno di essi si trova in un vertice del poliedro (regione ammissibile)
Programmazione lineare applicata in Hotel
Ma ora vediamo un esempio applicato all’ambito alberghiero:
Consideriamo un hotel chiamato “Hotel Blog” con i profili tariffari (con i che va da 1 a n). Consideriamo p_i il prezzo relativo ad ogni profilo tariffario, d_i la domanda attesa per il profilo tariffario i, x_i la capacità del profilo tariffario i e C la capacità totale di camere dell’hotel. Il problema per la massimizzazione del revenue sarà quindi scritto nel modo seguente:
Facciamo un esempio di Revenue Management attraverso l’uso della programmazione lineare. Immaginiamo il seguente scenario:
- Hote Blog ha 100 camere
- Il listino prezzi è suddiviso un 2 profili tariffari (pochi per diminuire il numero dei calcoli).
- La tariffa di bassa stagione è di 50 Euro.
- La tariffa di alta stagione invece è di 80 Euro
- La domanda per la tariffa di bassa stagione è 80 camere
- La domadna per la tariffa di alta stafione è di 60 camere
Il nostro povero albergatore ha un grande dilemma. Quante camere vendere alla tariffa alta e quanta alla tariffa bassa per massimizzare il profitto?
Vediamo come la programmazione lineare può aiutare il nostro albergatore.I dati da inserire nel modello sono (n=2, p1=80, d1=60, p2=50, d2=80, C=100) e il nostro problema di programmazione lineare si risolve in questo semplice modo:
Il risutlato del nostro problema è che si dovranno vendere 60 camere alla tariffa di alta stagione e 40 camere alla tariffa di bassa stagione. Qualcuno di voi si sarà messo a ridere perchè starà pensando che era ovvio il risultato! beh io concordo con quell’analisi ma dovete considerare il “modus operandi” e dovete verificare la bontà del risultato ottenuto per via geometrica dal nostro problemino di programmazione lineare. Poi considerate che l’esempio che abbiamo fatto è stato appositamente semplificato per poterlo risolvere per via geometrica senza diventare matti!! Aggiungete altri 3 o 4 vincoli e vedrete che a mente non sarà più cosi semplice!! 😉









Dietro questo semplice problema ce ne sono altri molto più interessanti e molto più difficili da modellare. Ad esempio, una prima estensione potrebbe essere quella di inserire tutta la parte che rappresenta i costi di gestione della domanda. Oppure rappresentare opportunamente l’incertezza presente nella previsione della domanda.
Esattamente!
Innanzitutto la ringrazio per aver lasciato il commento.
Detto questo, per quanto riguarda la parte dei costi non ci sono grossi problemi per l’implementazione di tutti i vincoli necessari.
La parte interessante e su cui si fonda tutto il sistema di Revenue Management è quella di rappresentare opportunamente la previsione della domanda. Ha qualche idea o suggerimento da proporre?
Sto preparando un articolo sul modello “bid Price” che si basa sul modellino descritto sopra ma lo complica un pochino e che dovrebbe aggiugere spunti interessanti alla discussione. Poi seguiranno gli articoli sulle altre tecniche utilizzate.
La sua esperienza nel campo della ricerca operativa è preziosa per la gestione ottimizzata delle vendite in hotel. Spero di poter contare su qualche suo prezioso spunto per sviluppare nuovi ragionamenti su questa disciplina che è ancora da approfondire ed in continuo divenire..
Ma alla fine mi sembra di capire che la funzione z=f(x,y) da massimizare è lineare in 2 variabili, pertanto è un piano nello spazio che è definito su un dominio chiuso e limitato che quindi ammette massimo e minimo.
Le camere non si dividono per stagione ma per livello di comfort, se si usassero numeri diversi da 80 euro e 80 camere l’esposizione diventerebbe più chiara.
Oramai la visione in 3D è di quotidiana trattazione quindi oltre ai diversi standard di comfort offerti + oltre alla inevitabile stagionalità (peraltro legata alla correlazione di costi stagionali ) + doverosamente considererei la variabile prezzo legata alla fluttuazione della domanda .