Approcci per l’analisi delle serie storiche

Gli approcci per l’analisi delle serie storiche hanno come obiettivo finale quello di individuare e rappresentare analiticamente la legge che regola l’andamento dei dati osservati, differiscono a seconda del modo in cui si intendono le “forze sottostanti” alla serie di dati presa in esame. Vediamo quali sono gli approcci utilizzati per quest’analisi.

Approccio classico o decompositivo

Tende ad individuare in una serie storica due componenti, una sistematica (o deterministica), ed una casuale. Tale impianto metodologico è finalizzato a scomporre la serie in singole componenti individuabili in maniera deterministica, e quindi “con certezza”. Ciò che del dato osservato non è spiegato dalla parte deterministica è invece ritenuto un “residuo” dovuto al caso.

Approccio moderno o stocastico

Viene proposto da Box e Jenkins nel 1976 (Box, Jenkins, & Reinsel, 1994); l’obiettivo di questa analisi è tentare di riprodurre il processo stocastico che si suppone abbia generato la serie storica, ossia l’insieme delle “forze” che hanno concorso a produrre il dato secondo leggi probabilistiche.

Approccio spettrale o frequenziale

Il più utilizzato prima della diffusione della metodologia di Box e Jenkins, è basato su un’analisi descrittiva della serie temporale osservata. Nello specifico la metodologia si basa sullo sviluppo delle serie di Fourier. Nell’articolo del 1807 presentato all’accademia delle Scienze di Parigi, Fourier intende risolvere il problema della non derivabilità di una serie attraverso la scomposizione di questa in funzioni derivabili. Ciascuna serie storica può pertanto intendersi come concettualmente formata da una serie infinita di “onde” sinusoidali e cosinusoidali (funzioni derivabili) ciascuna caratterizzata da una frequenza ω ed ampiezza dF(ω).

In questo articolo  saranno delineati (e utilizzati) i fondamenti teorici dell’approccio classico, per l’approccio moderno sarà solo delineate la ratio sottostante.

L’approccio classico all’analisi delle serie storiche

Secondo l’approccio classico una serie storica di dati è generata dall’interazione di componenti individuabili “ meccanicamente” a partire dai dati (componente deterministica o sistematica), che producono il dato con esattezza a meno di una componente erratica attribuibile al caso. Scopo di tale metodologia è quindi quello di scomporre la serie nelle singole “forze” della parte deterministica che hanno concorso alla formazione del dato; la parte del dato al netto della parte deterministica è una componente residuale aleatoria:

Ciascun dato Y_t è pertanto funzione (g) “dell’interazione” (espressa da segno”+”) di due elementi:

Una prima parte è funzione del tempo f(t) (la componente sistematica o deterministica), visto che si protrae “sistematicamente” per l’intervallo temporale oggetto dell’analisi in maniera regolare e come già detto può essere individuabile meccanicamente a partire dai dati;

Individuata la componente deterministica, rimane la seconda parte ε_t che esprime tutto ciò che la relazione deterministica non riesce a spiegare (è pertanto un “residuo” del tutto depurato dalla componente sistematica). Essa è chiamata componente erratica, aleatoria o casuale in quanto di ritiene prodotta dal caso.

La componente deterministica

La parte deterministica di una serie storica comprende tre elementi in relazione tra loro, che dipendono, direttamente o indirettamente, dal tempo. Prendendo come esempio la serie storica delle RoomNights del data base QU2 possiamo individuare:

Nel lungo periodo il numero di roomnights è leggermente aumentato: ciò si deduce dall’andamento tendenzialmente crescente (seppur di poco) della serie:

Ne breve periodo vi sono forti oscillazioni e si può notare una cadenza periodica (il calo delle roomnights durante gli ultimi mesi dell’anno) nei mesi che vanno da ottobre a novembre degli anni 2007, 2008 e 2009, i dati 2010 invece non sono disponibili.

Da queste osservazioni fatte in via preliminare analizzando il grafico sul lungo e sul breve periodo abbiamo ricavato 2 delle 3 possibili componente della parte deterministica:

La componente tendenziale, trend o componente evolutiva (T) rappresenta l’andamento che il fenomeno segue nel lungo periodo. Il trend è pertanto legato agli aspetti che influiscono sugli elementi “strutturali” che determinano un fenomeno.

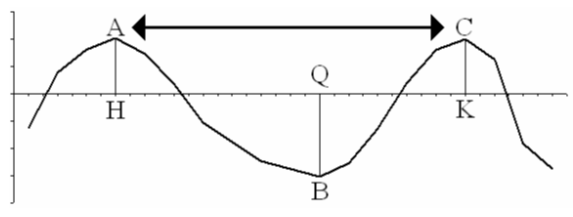
La componente ciclica, ciclo, o componente congiunturale (C) è la fluttuazione associata a fasi decrescenti di un fenomeno (che corrispondono rispettivamente a periodi di recessione ed espansione), di durata pluriennale. Perché si possa parlare di ciclo economico l’alternanza di tale fasi deve essere diffusa ( e quindi riguardante un ampio numero di attività economiche) e ricorrente. Riguardo alla durata , si suole distinguere il ciclo di lungo periodo o di Kuznets (circa 20 anni), il ciclo di medio periodo o di Juglar (7-11 anni), il ciclo di breve periodo o di Kitchin (circa 3,5 anni). In relazione alle cause che determinano il ciclo, si distingue la teoria esogena, per la quale il ciclo è determinato da elementi esterni ad un sistema economico (ad esempio, le vicende politiche, le innovazioni tecnologiche o l’andamento demografico), e la teoria endogena, per la quale le forze che determinano il ciclo economico sono interne al sistema (classico esempio è dato dall’influenza della produttività, fattore caratteristico del sistema economico) (Notarstefano, 2003). Per comprendere le fasi di un ciclo economico, si faccia riferimento alla figura sottostante. La distanza che intercorre tra due punti di svolta superiore, o di picco (si parla di distanza peack-to-peack), espressa nell’unità di tempo in cui è rilevato il fenomeno, è detta periodo (indica quindi la durata del ciclo. Il periodo è talvolta rilevato con riferimento alla distanza tra due punti di svolta inferiore, o di sella (si parla di distanza trough-to-trough). La variabile Y presenta un punto di picco al tempo t quando:

Specularmente, la variabile Y presenta un punto di sella al tempo t quando:

I punti di picco (A e C nell’esempio rappresentano punti di crisi, poiché a partire da questi la variabile inverte il suo andamento crescente. Specularmente i punti di minimo (B nell’esempio) rappresentano punti di ripresa, ossia il momento a partire dal quale la tendenza a decrescere si inverte. Il tratto intercorrente tra un punto di picco di una serie es il successivo punto di minimo rappresenta la fase di recessione (AB). Il tratto intercorrente , invece, tra un punto di minimo ed il successivo punto di picco rappresenta la fase di espansione (BC) (Alvaro, 1999).

La componente stagionale (S) è data da movimenti infra-annuali tipici dovuti a fattori di calendario, sociali, economici, climatici o organizzativi.

Identificazione

Dopo aver idealmente scomposto il dato nelle quattro componenti tendenziale, ciclica, stagionale e casuale occorre specificare la natura della relazione che lega gli elementi della parte deterministica e la parte aleatoria, passo necessario per le successive analisi. Occorre, cioè, identificare un modello a cui ricondurre la relazione della formula:

della quale renderemo esplicita la relazione tra le due componenti sommariamente espressa dal segno “+”. L’approccio classico considera essenzialmente tre modelli:

Modello Additivo

Il modello additivo presuppone che le componenti che lo hanno generato siano tra di loro indipendenti, ipotesi notevolmente semplificatrice giacché nella realtà ciascun fenomeno è il risultato della complessa interazione tra le forze di un sistema. In un modello additivo il trend T è espresso nella stessa unità di misura della variabile Y, mentre le restanti componenti esprimono variazioni assolute. Ad esempio, se la produzione di un bene nel mese di febbraio nell’anno t è pari a 1800 unità, quando la componente tendenziale è pari a 2300, la componente ciclica incide negativamente per 800, la componente stagionale influisce positivamente per 300 unità, mentre l’effetto della componente casuale è così basso da essere trascurabile, si ha la relazione:

1800=2300-800+300

Modello Moltiplicativo

dal quale si può passare al precedente attraverso una trasformazione logaritmica:

Il modello moltiplicativo presuppone che le componenti siano tra di loro interdipendenti. In esso è il solo trend ad essere espresso nella stessa unità di misura della variabile Y, mentre le restanti componenti sono espresse da numeri indice.

Misto, costituito da una combinazione dei precedenti, come ad esempio:

Dopo aver descritto per linee essenziali i fondamenti dell’approccio classico, rivolgiamo la nostra attenzione agli strumenti che permettono di scomporre le serie storiche nelle componenti sovrastanti.

Stima del Trend-Ciclo

Nonostante le componenti tendenziale e ciclica siano state sinora trattate separatamente, gli strumenti di seguito proposti deputati alla loro stima le trattano congiuntamente: il ciclo viene pertanto visto quale elemento caratteristico della tendenza di lungo periodo. (Guarini & Tassinari, 1990) distinguono 2 gruppi di metodologie:

Il primo tende a trattare principalmente i dati interessati da stagionalità; rientrano in tale gruppo il metodo delle medie mobili semplici ed il metodo dei rapporti lordi e netti di stagionalità;

Il secondo considera serie storiche in cui non sia presente la componente stagionale, e tra questi rientrano il metodo analitico ed il metodo delle medie mobili ponderate;

L’individuazione attraverso la rappresentazione grafica

Perché in una serie storica sia presente un trend è necessario che nel lungo periodo persista un regolare andamento di fondo: per tale motivo una prima modalità per desumere le caratteristiche della componente tendenziale è quella grafica. La maniera più intuitiva per descrivere sommariamente la tendenza di lungo periodo è difatti quella di tentare di interpolare graficamente una curva tra i punti di una serie storica secondo il loro andamento globale di lungo periodo, e tentando di rendere minima la distanza tra questa e le osservazioni.

Il metodo delle medie mobili

Uno dei metodi per depurare una serie storica di dati infrannuali dalla componente stagionali è l’utilizzo delle medie mobili semplici.

L’applicazione ad una serie storica della media mobile semplice centrata ha l’obiettivo di lisciare la serie e ridurne la variabilità. Perché ciò avvenga, k può essere scelto considerando il numero di sub-periodi compresi nel periodo di riferimento. Ad esempio, se si hanno a disposizione dati giornalieri di più anni e si cerca di ricavare la componente tendenziale-ciclica annuale del fenomeno, affinché sia “coperto” l’intero anno occorre che k=365, se invece si hanno dati mensili k=12, se quadrimestrali k=4. Questo è per far in modo che la componente stagionale si compensi in media nell’arco del periodo di riferimento.

Ciascuna media mobile va sostituita al dato su cui essa è centrata, ossia sul termine centrale dei dati su cui essa è calcolata. E’ intuibile attribuire la centratura nel caso in cui k è dispari: il nuovo dato si riferirà al termine centrale . Ad esempio, data la seguente serie di dati trimestrali, relativi a tre anni:

su cui calcoliamo la media mobile di ordine 3, se la media mobile centrata sul termine j-esimo è data z_k=(a_h+a_k+a_l)/3, essendo a_h a_k a_l termini successivi con h<k<l, la nuova serie sarà data da:

Si noti che la serie presenta un numero di osservazioni inferiore rispetto alla serie originaria. Ciò è ovviamente dovuto al fatto che non è possibile calcolare una media mobile centrata a 3 termini sul primo e sull’ultimo termine.

Nel caso in cui k sia pari non si ha un valore centrale a cui intuitivamente riferire la media. In questo caso occorre calcolare in un primo momento le medie mobili non centrate, e successivamente centrarle applicando a coppie successive di queste ultime un’ulteriore media mobile. Sia data, ad esempio, una serie di dati semestrali, relativi a tre anni:

Se volessimo determinare i valori del trend-ciclo annuali, è necessario in primo luogo calcolare una media mobile non centrata a 2 termini, che indichiamo genericamente con z_(h,k)=(a_h+a_k)/2,

essendo a_h a_k termini successivi con h<k (la media mobile non centrata a due termini è pertanto data da z_1,2 z_2,3 z_3,4 z_4,5 z_5,6). Successivamente, per centrare la media mobile ad esempio sul secondo termine occorrerà considerare:

Naturalmente il medesimo procedimento si adopera per gli altri termini della serie, ricavando così z_2 z_3 z_4.

Nella figura sottostante la serie storica delle roomnights è sovrapposta con la relativa media mobile centrata a 183 termini. La nuova serie palesa un andamento più liscio rispetto a quella originaria, evidenziando cosi la componente tendenziale-ciclica.

Stima della componente stagionale

Una modalità operativa che può permettere di verificare in maniera immediata la presenza di stagionalità è quella grafica. Se in corrispondenza degli stessi periodi di ciascun anno i dati palesano un andamento simile allora saremo di fronte a una serie di dati che presentano la componente stagionale.

Per stimare la componente stagionale prendendo in considerazione un modello moltiplicativo (sarà la stessa metodologia utilizzata per la comparazione dei modelli di forecasting alberghiero per il revenue managament illustrata in seguito):

Per il quale vogliamo quantificare l’effetto della componente stagionale al sub-periodo j (ad esempio mese) del periodo (ad esempio, anno) i, rapportando ciascun dato Y_ij al valore che la componente tendenziale-ciclica assume nel relativo periodo:

Otteniamo una buona stima della componente stagionale al lordo della componente aleatoria e se rapportiamo il modello moltiplicativo per questa componente otteniamo il Rapporlo Lordo di Stagionalità:

Alvaro (Alvaro, 1999) evidenzia che per la determinazione di Z_ij non è infrequente l’impiego della media mobile aritmetica, anche se per motivi di “coerenza formale e sostanziale” è più corretto impiegare la media mobile geometrica.

Dopo aver opportunamente sostituito i valori anomali si procede alla verifica della tendenza dei RLS relativi al periodo j di tutti gli anni della serie, attraverso, ad esempio, la rappresentazione grafica attraverso un diagramma cartesiano.

Se tali indici sono interpolabili da una retta parallela all’asse delle ascisse si ha il caso della stagionalità costante: la media aritmetica di tutti gli indici relativi ad uno stesso periodo è detta rapporto netto di stagionalità – 〖RNS〗_j – (quindi nel caso di dati mensili si avranno dodici indici nel caso di dati semestrali se ne avranno due, e così via), in quanto depurato dalla componente accidentale che pertanto si presume essere pari agli scarti di ciascun RLS dalla media “RNS”. Tutti i RLS al periodo j per tutti gli anni i avranno pertanto un solo RNS. La somma dei rapporti netti di stagionalità deve essere pari a k, in quanto in media la stagionalità deve essere “neutrale” in ciascun sub-periodo, essendo l’evoluzione del fenomeno legata esclusivamente al trend-ciclo. Se così non fosse, occorre correggere opportunamente i RNS in modo da ottenere k.

Nel caso in cui i rapporti lordi fossero interpolabili da una retta non parallela all’asse delle ascisse, e quindi, ad esempio, nel mese j-esimo di tutti gli anni il fenomeno presenta un’influenza crescente della stagionalità, si ha il caso della stagionalità variabile: a ciascun RLS sarà riferibile un proprio RNS espresso dall’equazione della retta:

〖RNS〗_t=a+bt

dove t rappresenta il trend. A differenza di quanto visto in precedenza non esisterà, pertanto, un solo coefficiente che esprime la stagionalità.

Poiché i RNS esprimono in percentuale l’influenza della componente stagionale sul fenomeno, costituiscono di fatto una delle modalità per pervenire alla destagionalizzazione della serie. Da ciò, rapportando ciascun dato al relativo RNS si ottiene un valore depurato dalla componente stagionale.