Goodness of Fit: la misura dell’errore nel Revenue Management
Come calcolare la percentuale d'errore nel forecasting alberghiero (forecast accuracy)

In molte analisi statistiche in cui un modello viene adattato a un set di dati, il termine accuratezza si riferisce alla capacità del modello di riprodurre i dati sui quali è stato stimato e cioè della bontà di adattamento del modello (Misura errore – goodness of fit).
L’accuratezza nella previsione (forecast accuracy), invece, misura la capacità del modello a riprodurre i dati futuri della serie.
Se il metodo di previsione si propone un orizzonte temporale di più periodi, la verifica della sua capacità previsiva può avvenire come di seguito indicato:
- Si utilizzano i primi m dati della serie per la stima del modello
- Si usano i successivi m+1,..,n dati per la verifica dell’accuratezza di previsione
La differenza fra l’errore di stime et e l’errore previsionale ft, può essere apprezzata mediante le formule seguenti:
Dove:
- y_1,y_2,…,y_n indica la serie di dati disponibili;
- y_1,y_2,…,y_m con m<n indica la serie di dati che viene usata per la stima del modello di previsione (trainig sample);
- y_(m+1),y_(m+2),…,y_n indica la serie di dati che viene usata per la veridica della capacità di previsione (test sample)
- y^_1,y^_2,…,y^_m sono le stime dei valori del training sample ottenute tramite il modello stimato;
- F_(m+1),F_(m+2),…,F_m sono le previsioni (forecast) riferite al periodo di tempo da t=m+1 a t=n (test sample), ottenuto tramite il modello stimato sul training sample.
Previsione a un passo
Spesso il decisore è interessato a conoscere il valore della serie relativa al periodo immediatamente successivo all’ultimo dato disponibile. Si tratta della previsione a un passo (one step forecast) che consiste nella previsione di un periodo in avanti rispetto all’ultima osservazione.
Ogni previsione F_t viene determinata pertanto usando i t-1 dati precedenti: y_1,y_2,…,y_(t-1) e cioè impiegando un modello di previsione che è stimato sui primi t-1 elementi della serie. Il procedimento è semplificato facendo riferimento al quadro riportato qui di seguito.
| Passi | Serie per la stima | One-stp forecast | Errore di previsione |
| 1 | y_1,y_2,…,y_H | F_(H+1) | y_(H+1)-F_(H+1) |
| 2 | y_1,y_2,…,y_H,y_(H+1) | F_(H+2) | y_(H+2)-F_(H+2) |
| … | … | … | … |
| … | … | … | … |
| n-1 | y_1,y_2,…,y_H,y_(H+1),y_(n-1) | F_n | y_n-F_n |
Partendo da un punto t=H>1 il modello viene stimato aggiungendo via via un nuovo elemento fino a t=n-1; si ottengono complessivamente n-H previsioni in corrispondenza dei periodi a partire da H+1 fino a n. In presenza di stagionalità, questo procedimento necessita di una serie adeguatamente lunga. Infatti, l’individuazione e la modellazione della stagionalità richiede di norma almeno 5 anni completi. Nel caso di dati mensili, ad esempio, H deve essere per lo meno superiore a 60 (12*5).
Vediamo infine le misure di bontà di adattamento/previsione usate più frequentemente (rispettivamente per la bontà di adattamento e di previsione):
- Errore Medio (MA); media aritmetica degli errori:
- Errore quadratico Medio (MSE); media aritmetica dei quadrati degli errori:
- Deviazione standard dell’errore (RMSE); la radice quadrata dell’MSE:
- Errore medio assoluto (MAE); media aritmetica degli errori presi in valore assoluto:
- Errore medio percentuale (MPE); media aritmetica degli errore relativi moltiplicati per 100:
- Errore medio assoluto percentuale (MAPE); media aritmetica degli errori relativi, presi in valore assoluto e moltiplicati per 100:
L’errore medio MA è una statistica intuitiva dato che rappresenta l’errore medio. Si noti però che errore in eccesso ad errori in difetto si compensano nella media. Per cui un basso valore di MA non garantisce che l’errore sia piccolo. Tale indice è infatti una misura del “bias”, ovvero da un’idea della distorsione della previsione: se MA>0 la previsione è tendenzialmente in eccesso se MA<0 la previsione è tendenzialmente in difetto.
Il fenomeno della compensazione fra errori in eccesso ed in difetto è cancellato dall’errore medio assoluto MAD che si calcola infatti come la media dei valori assoluti dell’errore. Tale indicatore rappresenta pertanto la media della magnitudine dell’errore e d analizza il fenomeno della consistenza. Anche l’errore quadratico medio MSE cancella la compensazione fra sovra e sotto stime ed è assimilabile alla varianza dell’errore. Inoltre, in termini statistici lo MSE rappresenta una misura più significativa e corretta dell’errore di previsione rispetto al MAC. Generalmente si cerca quindi la tecnica previsionale che minimizza tale misura. Lo stesso discorso vale per lo RMSE che, rispetto al MSE ha il vantaggio di essere espresso nella stessa unità di misura con cui è valutato l’errore.
Il mio preferito
L’errore percentuale MAPE (steso discorso per lo MPE) serve invece a valutare la bontà di un modello di previsione con serie di dati differenti. Infatti se si utilizzasse il MAE, si darebbe un peso maggiore ad un errore effettuato in un periodo in cui la domanda è elevata: l’errore relativo è basso, ma l’errore assoluto è alto. Pertanto, per evitare tale problematico è stato introdotto il MAPE.
Il nostro Forecasting alberghiero è accurato oppure no?
A questo punto ci chiediamo, come sia possibile stabilire se un sistema previsionale funzioni bene oppure no. Chiaramente non ci aspettiamo che la previsione sia perfetta, ma che sia almeno accurata; allora il problema diventa quello di stabilire se la previsione è accurata oppure no.
In linea teorica, data una serie storica composta dalla somma di più patter a cui si sovrappone un errore casuale, un modello ottimale dovrebbe essere in grado di riprodurre fedelmente tutti i pattern della domanda. In tal caso, nel lungo termine, l’errore di previsione MSE derivante dall’applicazione del modello tenderà esattamente all’errore casuale di cui è affetta la serie storica.
Il valore dello MSE sarebbe allora quello minimo teorico dato che rappresenterebbe esattamente la varianza dell’errore casuale. Il gap fra MSE e varianza dell’errore casuale rappresenta allora il parametro (teorico) di confronto per stabilire la bontà di un modello previsionale. Purtroppo il più delle volte ciò è impossibile dato che non si conosce nel il processo che genera la serie storica, ne la distribuzione statistica dell’errore casuale.
In questi casi è solo possibile confrontare i vari modelli sui dati disponibili e scegliere quello che minimizza l’errore, pur non potendo asserire con sicurezza che tale modello sia il migliore possibile. In genere, anche se tali valori dipendono dal contesto operativo, un modello che porta valori del MAPE dell’ordine del 10-15% sono già molto buoni.
E le vostre percentuali di errore per il forecasting alberghiero a quanto ammontano?




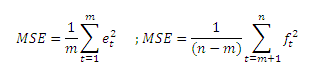
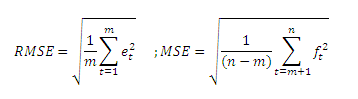

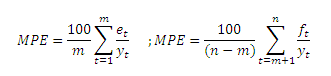
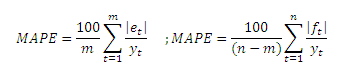




Molto interessante!
Ma nei fatti come faccio a calcolare la percentuale di errore?
Grazie Michela
Ciao Michela!
Ho aperto un forum in cui si faranno molti esempi su come utilizzare e come applicare il Revenue Management a casi reali!
Segui il forum e faremo di sicuro esempi sulla misura dell’errore!
Ciao
Edoardo